
题目列表(包括答案和解析)
6. (文科) 为了得到函数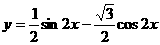 的图象,可以将函数
的图象,可以将函数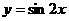 的图象 ( )
的图象 ( )
A.向左平移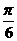 个单位长度 B.向右平移
个单位长度 B.向右平移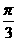 个单位长度
个单位长度
C.向右平移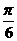 个单位长度 D.向左平移
个单位长度 D.向左平移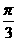 个单位长度
个单位长度
(理科)若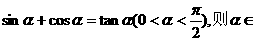 ( )
( )
A.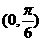 B.
B.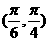 C.
C.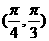 D.
D.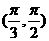
5.已知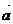 、
、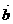 是非零向量且满足
是非零向量且满足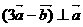 ,
,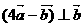 ,则
,则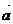 与
与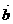 的夹角是( )
的夹角是( )
A.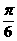 B.
B.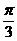 C.
C. D.
D.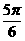
4、函数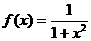 (
(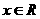 )的值域是( )
)的值域是( )
A.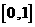 B.
B.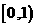 C.
C.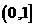 D.
D.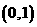
3. (文科)在等差数列{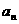 }中,
}中,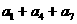 =45,
=45,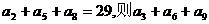 = ( )
= ( )
A.22 B.20 C.18 D.13
(理科)等比数列{an}中,已知对任意正整数n,a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2等于
( )
A、(2n-1)2 B、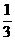 (2n-1) C、4n-1
D、
(2n-1) C、4n-1
D、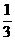 (4n-1)
(4n-1)
2、函数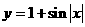 的图象( )
的图象( )
A.关于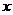 轴对称 B.关于
轴对称 B.关于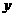 轴对称 C.关于原点对称
D.关于直线
轴对称 C.关于原点对称
D.关于直线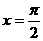 对称
对称
1.设集合M={1,2},N={2,3},集合P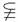 (M∪N),则P的个数是 ( )
(M∪N),则P的个数是 ( )
A. 6 ; B. 8 ; C. 7 ; D. 5 .
21.(14分)设函数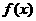 的定义域与值域均为R,
的定义域与值域均为R,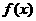 的反函数为
的反函数为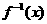 ,定义数列{
,定义数列{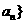 中,
中,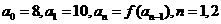 ,……。
,……。
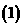 若对于任意实数x,均有
若对于任意实数x,均有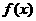 +
+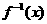 =2.5x,求证:①
=2.5x,求证:①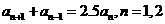 ,……。
,……。
②设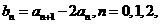 ……,求{
……,求{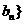 的通项公式。
的通项公式。
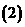 若对于任意实数x,均有
若对于任意实数x,均有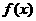 +
+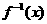 <2.5x,是否存在常数A、B同时满足:
<2.5x,是否存在常数A、B同时满足:
①当n=0.or.n=1时,有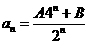 成立;②当n=2、3、4、……,时,
成立;②当n=2、3、4、……,时,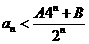 成立。
成立。
如果存在,求出A、B的值;如果不存在,说明理由。
20.(本题满分13分)
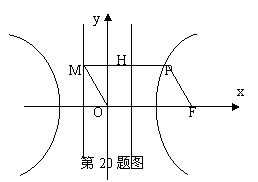 如图,F为双曲线C:
如图,F为双曲线C: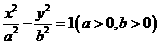 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于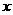 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形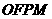 为平行四边形,
为平行四边形,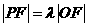 。
。
(Ⅰ)写出双曲线C的离心率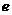 与
与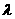 的关系式;
的关系式;
(Ⅱ)当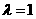 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若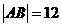 ,求此时的双曲线方程。
,求此时的双曲线方程。
19.(12分)有一个受到污染的湖泊,其湖水的容积为V立方米,每天流入流出湖泊的水量都是r立方米,现假设下雨与蒸发正好平衡,且污染物质与湖水能很好地混合,用g(t)表示第t天每立方米湖水所含污染物质的克数,我们称g(t)为第t天的湖水污染质量分数,已知目前每天流入湖泊的水中有p克的污染物质污染湖水,湖水污染物质分数满足关系式: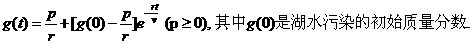 。
。
 当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
 求证:当
求证:当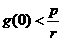 时,湖泊的污染程度越来越严重。
时,湖泊的污染程度越来越严重。
(3)如果政府加大治污力度,使得流入湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时的污染水平的5%?
18.(12分)甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
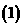 设
设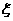 是前三次摸球中,甲摸到的红球的次数,求随机变量
是前三次摸球中,甲摸到的红球的次数,求随机变量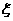 的概率分布与期望。
的概率分布与期望。
 在前四次摸球中,甲恰好摸中两次红球的概率。
在前四次摸球中,甲恰好摸中两次红球的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com