
题目列表(包括答案和解析)
2.删去数学归纳法在三角及不等式中的应用。
本章内容主要包括数学归纳法、极限。
㈠数学归纳法
演绎和归纳是数学推理的两种方法。归纳常常是发现问题的方法,演绎通常是严格证明的方法。数学归纳法起源于如何证明数学猜想的研究,而这些猜想多数是来源于归纳法。法国数学家帕斯卡在研究二项展开式时引进推理模式后,人们始称这一模式为娄学归纳法。数学归纳法是完全归纳法,它依据的原理是皮亚诺公理,是数学中最常用的一种归纳方法。
1.保留原教材数学归纳法的主要内容。
1)主要内容包括:归纳法及其不足,数学归纳法原理及步骤,数学归纳法在证明等式、整除性问题和几何问题中的应用。
2)以上内容在教材中的展开次序不变。
3)原教材在以上三类应用范围内的例题、练习和习题原则上保留下来的同时,又新增加了部分习题,如P68第七题、P101参考例题、P104复习参考题二中的第一题等,可见加强了这三类问题的应用。
2.6函数的连续性……………………………………………1课时
小结与复习……………………………………………………2课时
2.5极限的四则运算…………………………………………1课时
2.4函数的极限………………………………………………2课时
2.3数列的极限………………………………………………1课时
2.2研究性学习课题:杨辉三角……………………………3课时
8.设函数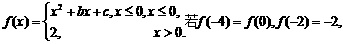 则关于x的方程
则关于x的方程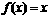 解的个数
解的个数
A.1 B.2 C.3 D.4
班别 姓名 学号 评分
7.函数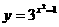
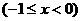 的反函数是
的反函数是
(A)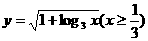 (B)
(B)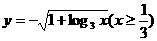
(C)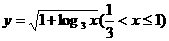 (D)
(D)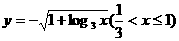
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com