
题目列表(包括答案和解析)
4.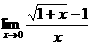 等于( B )
等于( B )
A. 1 B. 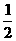 C. 0 D.
C. 0 D.
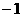
3.若ξ~ B(n, p),且Eξ=6,Dξ=3,则P(ξ=1)的值为( C )
A. 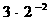 B.
B. 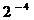 C.
C. 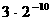 D.
D. 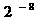
2.要从已编号(1-50)的50枚最新研制的某型号导弹中随机抽取5枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法,确定所选取的5枚导弹的编号可能是( B )
A. 5、10、15、20、25 B. 3、13、23、33、43
C. 1、2、3、4、5 D. 2、4、8、16、22
1.设随机变量ξ的分布列为P(ξ=i )=a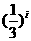 , i=1,2,3,则a的值为( D )
, i=1,2,3,则a的值为( D )
A. 1
B. 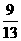 C.
C. 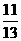 D.
D. 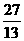
(17)(本小题满分12分)
编号为1、2、3的三位学生随意入座编号为1、2、3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的个数是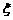 .
.
(Ⅰ)求随机变量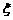 的概率分布;
的概率分布;
(Ⅱ)求随机变量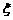 的数学期望和方差.
的数学期望和方差.
(18)(本小题满分12分)
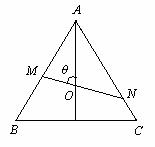
如图,已知在等边△ABC中,AB=3,O为中心,过O的直线交AB于M,AC于N,设
∠AOM=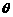 (60°≤
(60°≤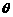 ≤120°),当
≤120°),当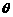 分别为何值时,
分别为何值时,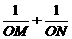 取得最大值和最小值.
取得最大值和最小值.
(19)(本小题满分12分)
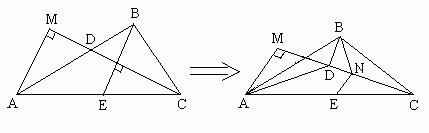
在△ABC中,CD为∠C的平分线,AC=4,BC=2,过B作BN⊥CD于N,延长
BN交CA于E,作AM⊥CD,交CD的延长线于M,将图形沿CD折起,使∠BNE
=120°.求:
(Ⅰ)折起后AM与BC所成的角;
(Ⅱ)折起后所得的线段AB的长度.
(20)(本小题满分14分)
已知数列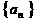 的通项为
的通项为 ,前n项和为
,前n项和为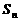 ,且
,且 是
是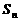 与2的等差中项;数列
与2的等差中项;数列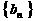
中,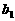 =1,点
=1,点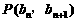 在直线x-y+2=0上.
在直线x-y+2=0上.
(Ⅰ)求数列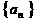 、
、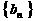 的通项公式;
的通项公式;
(Ⅱ)设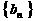 的前n项和为
的前n项和为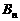 ,试比较
,试比较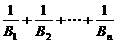 与2的大小;
与2的大小;
(Ⅲ)设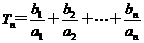 ,求
,求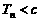 的最小整数c.
的最小整数c.
(21)(本小题满分12分)
一条斜率为1的直线l与离心率为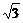 的双曲线
的双曲线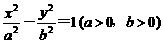 交于P、Q两点,
交于P、Q两点,
直线l与y轴交于R点,且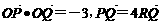 ,求直线与双曲线的方程.
,求直线与双曲线的方程.
(22)(本小题满分12分)
已知函数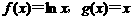 .
.
(Ⅰ)若x>1,求证: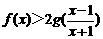 ;
;
(Ⅱ)是否存在实数k,使方程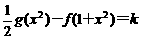 有四个不同的实根?若存在,
有四个不同的实根?若存在,
求出k的取值范围;若不存在,说明理由.





(13)i为虚数单位,复数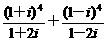 等于___________________.
等于___________________.
(14)求极限: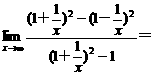 ____________________.
____________________.
(15)已知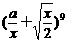 的展开式中
的展开式中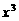 的系数为9,则常数a的值为_______________.
的系数为9,则常数a的值为_______________.
(16)已知函数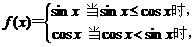 给出下列四个结论:
给出下列四个结论:
① 当且仅当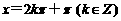 时
时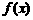 取得最小值;
取得最小值;
② 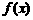 是周期函数;
是周期函数;
③ 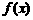 的值域是
的值域是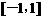 ;
;
④ 当且仅当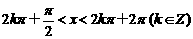 时
时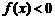 .
.
其中正确结论的序号是:___________________________.
(1)已知向量a=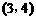 ,b=
,b=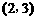 ,且(a+
,且(a+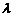 b)⊥(a-b),则
b)⊥(a-b),则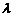 等于
等于
(A)1 (B)-1 (C)3 (D)-3
(2)如果森林区的森林蓄积量每年平均比上一年增长10.4%,那么经过x年可以增长到原来
的y倍,则函数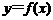 的图象大致为
的图象大致为
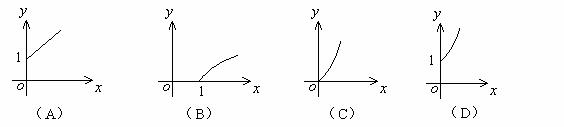
(3)若3个平面将空间分成m部分,则m的值为
(A)4 (B)4或6 (C)4或6或7 (D)4或6或7或8
(4)同一天内,甲地下雨的概率是0.15,乙地下雨的概率是0.12,假定在这天两地是否下雨
相互之间没有影响,那么甲、乙两地都不下雨的概率是
(A)0.102 (B)0.132 (C)0.748 (D)0.982
(5)已知F是抛物线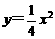 的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是
的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是
(A)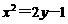 (B)
(B)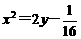 (C)
(C)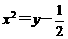 (D)
(D)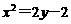
(6)已知条件p: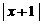 >2,条件q:5x-6>
>2,条件q:5x-6>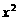 ,则
,则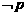 是
是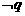 的
的
(A)充分必要条件 (B)充分非必要条件
(C)必要非充分条件 (D)既非充分又非必要条件
(7)直线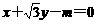 与圆
与圆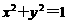 在第一象限内有两个不同的交点,则m的取值范围是
在第一象限内有两个不同的交点,则m的取值范围是
(A)1<m<2 (B)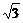 <m<3 (C)1<m<
<m<3 (C)1<m<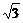 (D)
(D)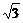 <m<2
<m<2
(8)已知函数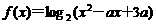 在区间
在区间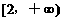 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是
(A)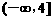 (B)
(B)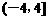
(C)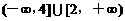 (D)
(D)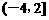
(9)若x>4,则函数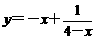
(A)有最大值-6 (B)有最小值6 (C)有最大值-2 (D)有最小值2
(10)设球O的半径为R,A、B、C为球面上三点,A与B、A与C的球面距离都为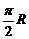 ,B与C的球面距离为
,B与C的球面距离为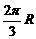 ,则球O在二面角B-OA-C内的那一部分的体积是
,则球O在二面角B-OA-C内的那一部分的体积是
(A)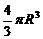 (B)
(B)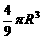 (C)
(C)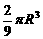 (D)
(D)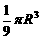
(11)将函数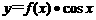 的图象按向量a=
的图象按向量a=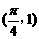 平移,得到函数
平移,得到函数 的图象,那么
的图象,那么
函数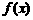 是
是
(A) (B)
(B) (C)
(C)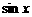 (D)
(D)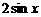
(12)已知符号函数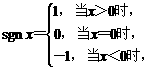 则方程
则方程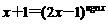 的所有解之和是
的所有解之和是
(A)0
(B)2
(C)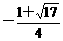 (D)
(D)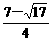
汕头市2004年普通高校招生模拟考试
数 学
第Ⅱ卷 (非选择题 共90分)
22.(本小题满分14分)
(文科做)已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1],a+b≠0有 >0.
>0.
(1)判断函数f(x)在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式f(x+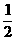 )<f(
)<f(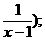
(3)若f(x)≤m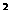 -2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
(理科做)二次函数y=ax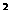 +x+1(a>0)的图象与x轴两个交点的横坐标分别为x
+x+1(a>0)的图象与x轴两个交点的横坐标分别为x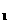 、x
、x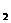 .
.
(1)证明(1+x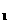 )·(1+x
)·(1+x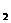 )=1;
)=1;
(2)证明x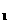 <-1,x
<-1,x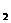 <-1;
<-1;
(3)若x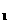 、x
、x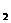 满足不等式|lg
满足不等式|lg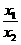 |≤1,试求a的取值范围.
|≤1,试求a的取值范围.
21.(本小题满分12分)
已知点P到两个定点A(1,0),B(2,0)的距离的比为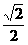 .
.
(1)求点P的轨迹C的方程;
(2)是否存在过点A(1,0)的直线l交轨迹C于M,N两点,使S =
=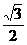 (O为坐标原点),若存在,求出l的方程;若不存在,说明理由.
(O为坐标原点),若存在,求出l的方程;若不存在,说明理由.
20.(本小题满分12分)
某商场预计全年分批购入每台价值为2000元的电视机共3600台,每批都购入x台(x∈N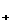 ),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运费和保管费43600元.现在全年只有24000元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运费和保管费43600元.现在全年只有24000元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com