
12、(江苏省常州市2008-2009高三第一学期期中统一测试数学试题)设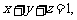 求
求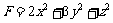 的最大值.
的最大值.
 7′
7′
当且仅当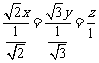 且
且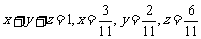
F有最小值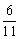 10′
10′
11、(福建省德化一中2009届高三上学期第三次综合测试)已知不等式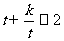 对
对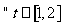 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
解:由不等式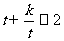 得
得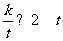 ,…………………………1分
,…………………………1分
又∵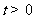 ∴
∴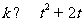 ,…………………………3分
,…………………………3分
对于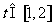 ,
,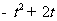 的最小值是0………………………5分
的最小值是0………………………5分
故要使得原不等式恒成立,只需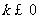 …………………………7分
…………………………7分
10、(福建省福州三中高三年级第二次月考)已知函数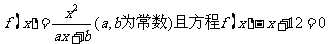 有两个实根为
有两个实根为
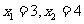 。
。
(1)求函数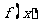 的解析式;
的解析式;
(2)设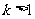 ,解关于
,解关于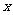 的不等式
的不等式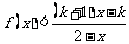 。
。
解:(1)依题意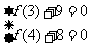 ………………2分
………………2分
∴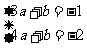 ……………………4分
……………………4分
解得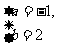 ……………………5分
……………………5分
∴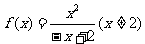 ……………………6分
……………………6分
(2)由(1)得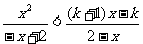
∴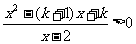
∴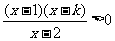 ………………8分
………………8分
①当k>2时, 或
或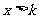
②当k=2时,
∴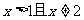
③当1<k<2时,1<x<k或x>2……………………11分
综上所述,当k>2时,不等式解集为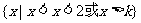
当k=2时,不等式解集为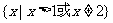
当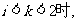 不等式解集为
不等式解集为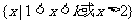 ………………12分
………………12分
9、(西南师大附中高2009级第三次月考)已知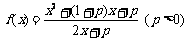
(1)若p > 1时,解关于x的不等式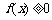 ;
;
(2)若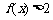 对
对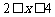 时恒成立,求p的范围.
时恒成立,求p的范围.
解:(1) 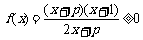 ······················································································ 1分
······················································································ 1分
①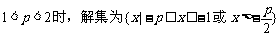 ········································ 3分
········································ 3分
② p = 2时,解集为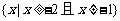 ····················································· 5分
····················································· 5分
③ p > 2时,解集为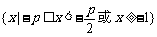 ··········································· 7分
··········································· 7分
(2) 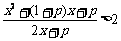
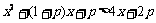 ··········································································· 8分
··········································································· 8分
∴ 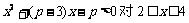 恒成立
恒成立
∴ 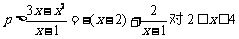 恒成立······································ 9分
恒成立······································ 9分
∵ 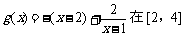 上递减·················································· 10分
上递减·················································· 10分
∴ 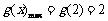 ················································································ 11分
················································································ 11分
∴ p > 2 ·································································································· 12分
8、(山东省平邑第一中学2009届高三元旦竞赛试题)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
(I)
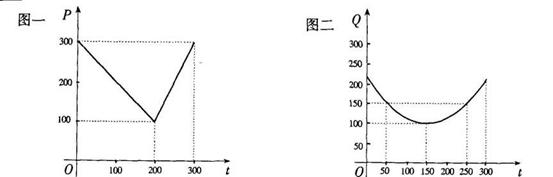 写出图一表示的市场售价与时间的函数关系式P=
写出图一表示的市场售价与时间的函数关系式P=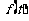 ;
;
写出图二表示的种植成本与时间的函数关系式Q=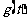 ;
;
(II) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/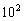 kg,时间单位:天)
kg,时间单位:天)
本小题主要考查函数图象建立的函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力。满分12分。
解:(I)由图一可得市场售价与时间的函数关系为
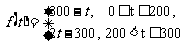
由图二可得种植成本与时间的函数关系为
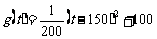 ,
, 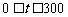
(II)设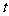 时刻的纯收益为
时刻的纯收益为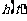 ,则由题意得
,则由题意得
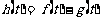 ,
,
即 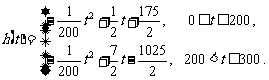
当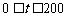 时,配方整理得
时,配方整理得
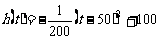 ,
,
所以,当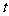 =50时,
=50时,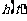 取得区间
取得区间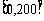 上的最大值100;
上的最大值100;
当 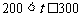 时,配方整理得
时,配方整理得
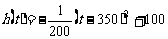 ,
,
所以,当 时,
时,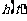 取得区间
取得区间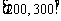 上的最大值87.5;
上的最大值87.5;
综上,由100>87.5可知,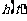 在区间
在区间 上可以取最大值100,此时,
上可以取最大值100,此时, 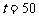 ,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
7、(湖南省衡阳市八中2009届高三第三次月考试题)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(1) 要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)
若|AN| 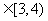 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
 解:设AN的长为x米(x >2)
解:设AN的长为x米(x >2)
∵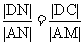 ,∴|AM|=
,∴|AM|=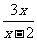
∴SAMPN=|AN|•|AM|=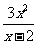
(1)由SAMPN
> 32 得 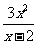 > 32 ,
> 32 ,
∵x >2,∴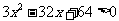 ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴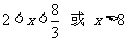 即AN长的取值范围是
即AN长的取值范围是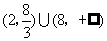
(2)令y=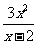 ,则y′=
,则y′=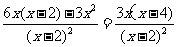
∵当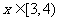 ,y′< 0,∴函数y=
,y′< 0,∴函数y=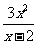 在
在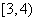 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=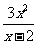 取得最大值,即
取得最大值,即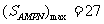 (平方米)
(平方米)
此时|AN|=3米,|AM|=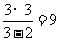 米
米
6、(四川省成都市高2009届高中毕业班第一次诊断性检测)已知函数f(x)=(x≠0,a>0,c<0),当x∈[1,3]时,函数f(x)的取值范围恰为[-,]
(1)求函数f(x)的解析式;
(2)若向量=(-,),=(k2+k+2,3k+1)(k>-1,且k≠0),解关于x的不等式f(x)<·
解:(1)f(x)=) ∵a>0,c<0,∴f '(x)=)>0 ∴函数f(x)在[1,3]上是增函数 ……3' 由 Þ a=2,c=-4 ∴f(x)=(x≠0) ……5' (2)∵·=- ……6' ∴f(x)<· ó <- ó < ó <0 ó <0 ……8' ∵k>-1,且k≠0,∴k+1>0 于是-1<k<0时,x∈(-∞,2k)∪(0,k+1) 0<k<1时,x∈(-∞,0)∪(2k,k+1) k=1时,x∈(-∞,0) k>1时,x∈(-∞,0)∪(k+1,2k) ……12'
5、(河北省衡水中学2008-2009学年度第一学期期中考试)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为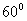 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为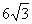 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.
(1) 求外周长的最小值,此时防洪堤高h为多少?
(2)
如防洪堤的高限制在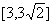 范围内,外周长最小为多少米?
范围内,外周长最小为多少米?
解:
(1)有题意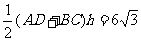 ,
,
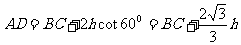
所以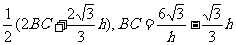
设外围周长为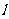 ,则
,则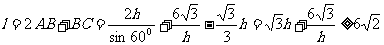
当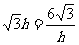 ,即
,即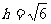 时等号成立.
时等号成立.
所以外围的周长的最小值为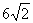 米,此时堤高
米,此时堤高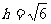 米.--------------8分
米.--------------8分
(2)由(1)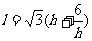 ,由导数或定义可证明在
,由导数或定义可证明在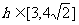 单调递增,
单调递增,
所以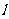 的最小值为
的最小值为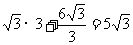 米(当
米(当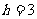 )-------------------12分
)-------------------12分
4、(广东省深圳中学2008-2009学年度高三第一学段考试)解不等式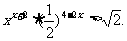
解:(1)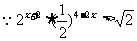
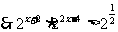
即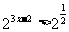 …………………………3分
…………………………3分
得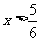 …………………………4分
…………………………4分
所以原不等式的解集为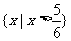 ……………………5分
……………………5分
3、(江西省南昌二中2008-2009学年度第一轮第二次段考)已知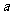 ,b为正数,求证
,b为正数,求证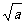 +1>成立的充要条件是对于任何大于1的正数
+1>成立的充要条件是对于任何大于1的正数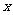 ,
,
恒有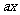 +
+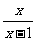 >b.
>b.
证明:⑴ax+=a(x-1)++1+a≥2+1+a=(+1)2>b;
⑵因为ax+>b对于大于1的实数x恒成立,即x>1,[ax+]min>b.
而ax+=a(x-1)++1+a≥2+1+a=(+1)2,
当且仅当a(x-1)=时,即x=1+>1时等号成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com