
题目列表(包括答案和解析)
5.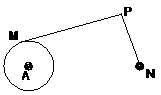 如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,过动点P作A的切线PM(M为切点),连结PN使得PM:PN=
如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,过动点P作A的切线PM(M为切点),连结PN使得PM:PN=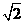 ,试建立适当
,试建立适当
的坐标系,求动点P的轨迹
4.已知圆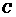 :
: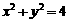 .
.
(1)直线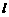 过点
过点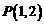 ,且与圆
,且与圆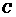 交于
交于 、
、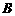 两点,若
两点,若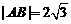 ,求直线
,求直线 的方程;
的方程;
(2)过圆 上一动点
上一动点 作平行于
作平行于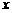 轴的直线
轴的直线 ,设
,设 与
与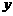 轴的交点为
轴的交点为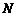 ,若向量
,若向量 ,求动点
,求动点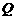 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
3.已知圆C: x2+y2-2x+4y-4=0,是否存在斜率为1的
直线L,使以L 被圆C截得弦AB为直径的圆
经过原点?若存在,写出直线的方程;若不存在,说
明理由
2.如图,设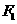 、
、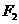 分别为椭圆
分别为椭圆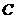 :
: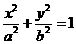 (
(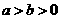 )的左、右焦点.
)的左、右焦点.
(Ⅰ)设椭圆C上的点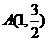 到F1、F2两点距离之和等于4,写出椭圆C的方程和离心率;
到F1、F2两点距离之和等于4,写出椭圆C的方程和离心率;
(Ⅱ)设点K是(Ⅰ)中所得椭圆上的动点,求线段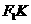 的中点的轨迹方程.
的中点的轨迹方程.

1.已知动圆过定点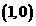 ,且与直线
,且与直线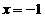 相切.
相切.
(1) 求动圆的圆心轨迹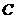 的方程;
的方程;
(2) 是否存在直线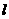 ,使
,使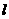 过点(0,1),并与轨迹
过点(0,1),并与轨迹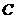 交于
交于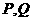 两点,且满足
两点,且满足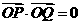 ?若存在,求出直线
?若存在,求出直线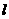 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
21.(本小题满分14分)
若存在实常数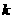 和
和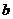 ,使得函数
,使得函数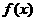 和
和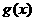 对其定义域上的任意实数
对其定义域上的任意实数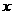 分别满足:
分别满足: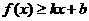 和
和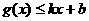 ,则称直线
,则称直线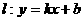 为
为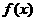 和
和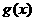 的“隔离直线”.已知
的“隔离直线”.已知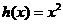 ,
,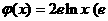 为自然对数的底数).
为自然对数的底数).
(1)求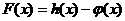 的极值;
的极值;
(2)函数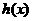 和
和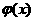 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
20. (本小题满分14分)
在直角坐标系 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线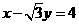 相切.
相切.
(1)求圆 的方程;
的方程;
(2)圆 与
与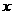 轴相交于
轴相交于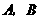 两点,圆内的动点
两点,圆内的动点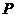 使
使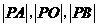 成等比数列,求
成等比数列,求 的取值范围.
的取值范围.
19.(本题满分14分)
已知函数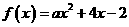 ,若对任意
,若对任意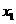 ,
, 且
且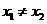 ,都有
,都有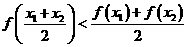 .
.
(1)求实数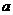 的取值范围;
的取值范围;
(2)对于给定的实数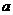 ,有一个最小的负数
,有一个最小的负数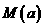 ,使得
,使得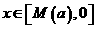 时,
时,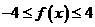 都成立,则当
都成立,则当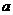 为何值时,
为何值时,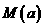 最小,并求出
最小,并求出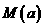 的最小值.
的最小值.
18.(本小题满分14分)
某个体户计划经销A、B两种商品,据调查统计,当投资额为x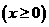 万元时,在经销A、B商品中所获得的收益分别为
万元时,在经销A、B商品中所获得的收益分别为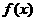 万元与
万元与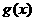 万元. 其中
万元. 其中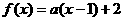 (
(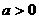 );
);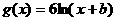 (
(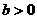 )已知投资额为零时,收益为零。
)已知投资额为零时,收益为零。
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据: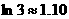 )
)
17. (本小题满分12分)
如图,已知多面体ABC-DEFG中,AB、AC、AD两两
互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,
AB=AD=DG=2,AC=EF=1,
(1)试判断CF是否与平面ABED平行?并说明理由;
(2)求多面体ABC-DEFG的体积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com