
2006年普通高等学校招生全国统一考试数学分类汇编
第二章《函数》
一、选择题(共40题)
1.(安徽卷)函数
 的反函数是
的反函数是
A.
 B.
B.
 C.
C.
 D.
D.

解:有关分段函数的反函数的求法,选C。也可用特殊点排除法,原函数上有(1,2)和(-1,-1)两点,反函数上有(2,1)和(-1,-1),检验知C。
2.(安徽卷)函数 的反函数是( )
的反函数是( )
A. B.
B.
C. D.
D.
解:由 得:
得: ,所以
,所以 为所求,故选D。
为所求,故选D。
3.(北京卷)已知 是
是 上的减函数,那么
上的减函数,那么 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C) (D)
(D)
解:依题意,有0<a<1且3a-1<0,解得0<a< ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³ 故选C
故选C
4.(北京卷)已知 是(-
是(-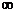 ,+
,+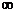 )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+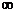 ) (B)(-
) (B)(-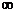 ,3) (C)[
,3) (C)[ ,3) (D)(1,3)
,3) (D)(1,3)
解:依题意,有a>1且3-a>0,解得1<a<3,又当x<1时,(3-a)x-4a<3-5a,当x³1时,logax³0,所以3-5a£0解得a³ ,所以1<a<3故选D
,所以1<a<3故选D
5.(北京卷)在下列四个函数中,满足性质:“对于区间 上的任意
上的任意 ,
, 恒成立”的只有
恒成立”的只有
(A) (B)
(B) (C)
(C) (D)
(D)
解: |
|
 >1
>1 <1\
<1\  |<|x1-x2|故选A
|<|x1-x2|故选A
6.(福建卷)函数y=┯
 (x?1)的反函数是
(x?1)的反函数是
A.y= (x>0) B.y=
(x>0) B.y=  (x<0) C.y=
(x<0) C.y= (x>0) D. .y=
(x>0) D. .y= (x<0)
(x<0)
解:对于x>1,函数 >0,解得
>0,解得 ,
, =
= ,∴ 原函数的反函数是
,∴ 原函数的反函数是 ,选A.
,选A.
7.(福建卷)函数 的反函数是
的反函数是
(A) (B)
(B)
(C) (D)
(D)
解:由函数 解得
解得 (y≠1),∴ 原函数的反函数是
(y≠1),∴ 原函数的反函数是 .
.
8.(福建卷)已知 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, 设
设
 则
则
(A) (B)
(B) (C)
(C) (D)
(D)
解:已知 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, 设
设 ,
,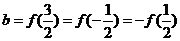 ,
, <0,∴
<0,∴ ,选D.
,选D.
9.(广东卷)函数 的定义域是
的定义域是
A. B.
B.  C.
C.
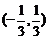 D.
D. 
解:由 ,故选B.
,故选B.
10.(广东卷)下列函数中,在其定义域内既是奇函数又是减函数的是
A. B.
B.  C.
C.  D.
D. 
解:B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇函数,是减函数;故选A.
 11.(广东卷)函数
11.(广东卷)函数 的反函数
的反函数 的图像与
的图像与 轴交于点
轴交于点
 (如图2所示),则方程
(如图2所示),则方程 在
在 上的根是
上的根是
A.4 B
解: 的根是
的根是 2,故选C
2,故选C
12.(湖北卷)设 ,则
,则 的定义域为
的定义域为
A. B.
B. C.
C. D.
D.
解:f(x)的定义域是(-2,2),故应有-2< <2且-2<
<2且-2< <2解得-4<x<-1或1<x<4
<2解得-4<x<-1或1<x<4
故选B
13.(湖北卷)关于 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.
解:关于x的方程 可化为
可化为 …(1)
…(1)
或 (-1<x<1)…………(2)
(-1<x<1)…………(2)
①
当k=-2时,方程(1)的解为± ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根
②
当k= 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根± ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根± ,即原方程恰有4个不同的实根
,即原方程恰有4个不同的实根
③
当k=0时,方程(1)的解为-1,+1,± ,方程(2)的解为x=0,原方程恰有5个不同的实根
,方程(2)的解为x=0,原方程恰有5个不同的实根
④
当k= 时,方程(1)的解为±
时,方程(1)的解为± ,±
,± ,方程(2)的解为±
,方程(2)的解为± ,±
,± ,即原方程恰有8个不同的实根
,即原方程恰有8个不同的实根
选A
14.(湖南卷)函数 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3, +∞) C.(4, +∞) D.[4, +∞)
解:函数 的定义域是
的定义域是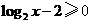 ,解得x≥4,选D.
,解得x≥4,选D.
15.(湖南卷)函数 的定义域是
的定义域是
A.(0,1] B. (0,+∞) C. (1,+∞) D. [1,+∞)
解:函数 的定义域是
的定义域是 ,解得x≥1,选D.
,解得x≥1,选D.
16.(江西卷)若不等式x2+ax+1³0对于一切xÎ(0, 〕成立,则a的取值范围是( )
〕成立,则a的取值范围是( )
A.0
B. ? D.-3
D.-3
解:设f(x)=x2+ax+1,则对称轴为x=
若 ³
³ ,即a£-1时,则f(x)在〔0,
,即a£-1时,则f(x)在〔0, 〕上是减函数,应有f(
〕上是减函数,应有f( )³0Þ
)³0Þ
- £x£-1
£x£-1
若 £0,即a³0时,则f(x)在〔0,
£0,即a³0时,则f(x)在〔0, 〕上是增函数,应有f(0)=1>0恒成立,故a³0
〕上是增函数,应有f(0)=1>0恒成立,故a³0
若0£ £
£ ,即-1£a£0,则应有f(
,即-1£a£0,则应有f( )=
)= 恒成立,故-1£a£0
恒成立,故-1£a£0
综上,有- £a故选C
£a故选C
17.(江西卷)某地一年的气温Q(t)(单位:ºc)与时间t(月份)之间的关系如图(1)示,已知该年的平均气温为10ºc,令G(t)表示时间段〔0,t〕的平均气温,G(t)与t之间的函数关系用下列图象表示,则正确的应该是( )

|